Type II string theory
| String theory |
|---|
| Superstring theory |
|
Related Topics
|
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings. These account for two of the five consistent superstring theories in ten dimensions. Both theories have the maximal amount of supersymmetry — namely 32 supercharges — in ten dimensions. Both theories are based on oriented closed strings. On the worldsheet, they differ only in the choice of GSO projection.
Contents |
Type IIA string
At low energies, type IIA string theory is described by type IIA supergravity in ten dimensions which is a non-chiral theory (i.e. left-right symmetric) with (1,1) d=10 supersymmetry; the fact that the anomalies in this theory cancel is therefore trivial.
In the 1990s it was realized by Edward Witten (building on previous insights by Michael Duff, Paul Townsend, and others) that the limit of type IIA string theory in which the string coupling goes to infinity becomes a new 11-dimensional theory called M-theory.
The mathematical treatment of type IIA string theory belongs to symplectic topology and algebraic geometry, particularly Gromov-Witten invariants.
Type IIB string
At low energies, type IIB string theory is described by type IIB supergravity in ten dimensions which is a chiral theory (left-right asymmetric) with (2,0) d=10 supersymmetry; the fact that the anomalies in this theory cancel is therefore nontrivial.
In the 1990s it was realized that type II string theory with the string coupling constant  is equivalent to the same theory with the coupling
is equivalent to the same theory with the coupling 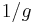 . This equivalence is known as S-duality.
. This equivalence is known as S-duality.
Orientifold of type IIB string theory leads to type I string theory.
The mathematical treatment of type IIB string theory belongs to algebraic geometry, specifically the deformation theory of complex structures originally studied by Kunihiko Kodaira and Donald C. Spencer.
Relationship between the type II theories
In the late 1980s, it was realized that type IIA string theory is related to type IIB string theory by T-duality.